
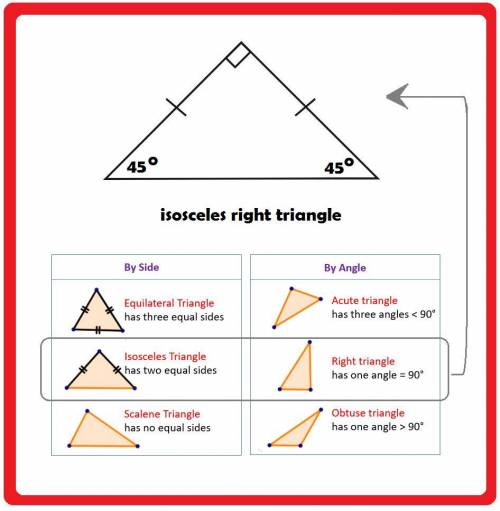
Frequently, complex or sophisticated forms are deconstructed into simpler ones, such as triangles. Numerous triangles found in the real world, like a part of a slice of pizza, can be called isosceles. Properties, Characteristics, and Applications of the Isosceles Triangle Isosceles Triangle TheoremsĪccording to the isosceles triangle theorem, if two sides of a triangle are congruent, then their opposing angles are likewise congruent. This article will cover the isosceles triangle theorem and its converse. In mathematics, the isosceles triangle theorem says that the angles opposite the equal sides of an isosceles triangle are also equal in measurement. We can see that the three angles in an isosceles triangle add up to 180°.An isosceles triangle has two sides of equal length and a third of varying length. We divide 150° into two equal parts to see what angle ‘a’ and ‘b’ are equal to. The size of these two angles are the same. We can subtract 30° from 180° to see what angle ‘a’ and ‘b’ add up to.Īnd so, angles ‘a’ and ‘b’ both add up to 150°.īecause angles ‘a’ and ‘b’ are both opposite the marked sides, they are equal to each other. This time, we know the angle that is not opposite a marked side. Here is another example of finding the missing angles in isosceles triangles when one angle is known.
We first add the two 50° angles together.Īngle ‘b’ is 80° because all angles in a triangle add up to 180°. To find angle ‘b’, we subtract both 50° angles from 180°. Now to find angle ‘b’, we use the fact that all three angles add up to 180°. This means that it is the same size as the angle that is opposite the other marked side. This angle is opposite one of the marked sides. Here is an example of finding two missing angles in an isosceles triangle from just one known angle. If the known angle is not opposite a marked side, then subtract this angle from 180° and divide the result by two to get the size of both missing angles.Add these two angles together and subtract the answer from 180° to find the remaining third angle. If the known angle is opposite a marked side, then the angle opposite the other marked side is the same.

If only one angle is known in an isosceles triangle, then we can find the other two missing angles using the following steps:
Base of isosceles triangle angles how to#
How to Find Missing Angles in an Isosceles Triangle from only One Angle We can also think, “What angle do we need to add to 70° and 70° to make 180°?” The missing angle on the top of this isosceles triangle is 40°. We subtract the 140° from 180° to see what the size of the remaining angle is. The missing angle is not opposite the two marked sides and so, we add the two base angles together and then subtract this result from 180 to get our answer.Īngles in an isosceles triangle add to 180°. The two base angles are opposite the marked lines and so, they are equal to each other. This is because all three angles in an isosceles triangle must add to 180°įor example, in the isosceles triangle below, we need to find the missing angle at the top of the triangle. If the missing angle is not opposite a marked side, then add the two angles opposite the marked sides together and subtract this result from 180.If the missing angle is opposite a marked side, then the missing angle is the same as the angle that is opposite the other marked side.

To find a missing angle in an isosceles triangle use the following steps: How to Find a Missing Angle in an Isosceles Triangle If we are told that one of these marked angles is 70°, then the other marked angle must also be 70°. The angle at which these two marked sides meet is the odd one out and therefore is different to the other two angles. The two equal angles are opposite to the two equal sides. The sides that are the same length are each marked with a short line. We can see that in this above isosceles triangle, the two base angles are the same size.Īll isosceles triangles have a line of symmetry in between their two equal sides. It has two equal sides marked with a small blue line. We can recognise an isosceles triangle because it will have two sides marked with lines.īelow is an example of an isosceles triangle.
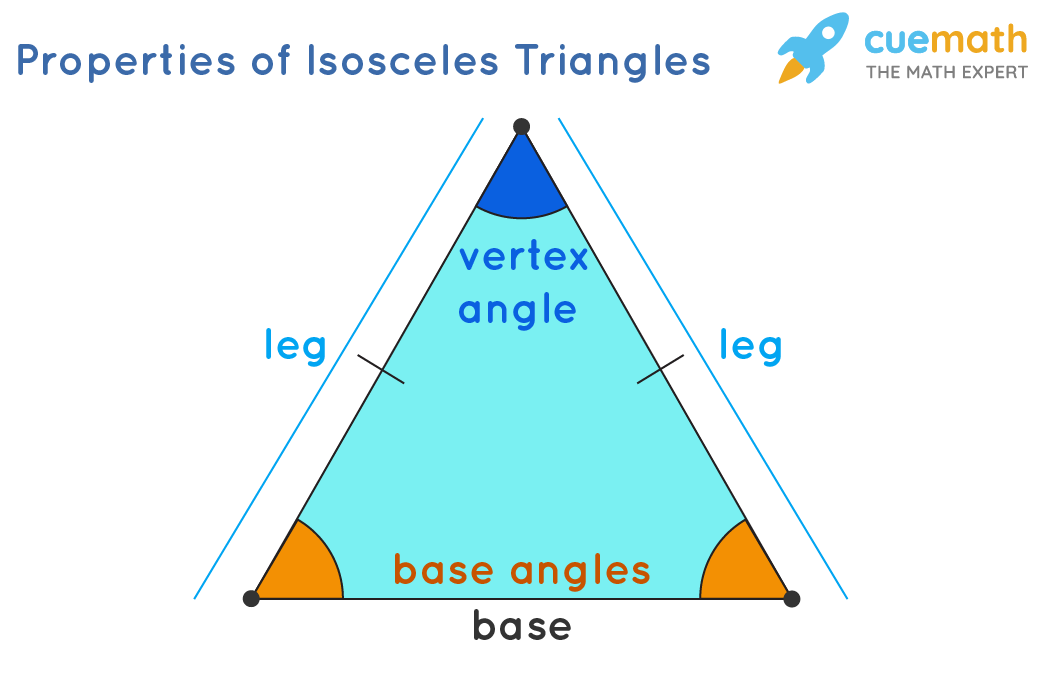
The two equal sides are marked with lines and the two equal angles are opposite these sides. An isosceles triangle is a triangle that has two equal sides and two equal angles.


 0 kommentar(er)
0 kommentar(er)
